In a recent entry, I mentioned the utmost importance of this subject: How can one find if a given rectangular measurement or multiplexing matrix has the property of allowing recoverability of sparse signals or unknowns. Most papers are currently using the convenient Restricted Isometry Property but it is thought that this is an unnecessarily tight property. Alexandre d'Aspremont and Laurent El Ghaoui have now updated to version 3 their preprint entitled: Testing the Nullspace Property using Semidefinite Programming. Because it is important work for the whole field, I am pasting the abstract again:Recent results in compressed sensing show that, under certain conditions, the sparsest solution to an underdetermined set of linear equations can be recovered by solving a linear program. These results rely on nullspace properties of the system matrix. So far, no tractable algorithm is known to test these conditions and most current results rely on asymptotic properties of sparse eigenvalues of random matrices. Given a matrix A, we use semidefinite relaxation techniques to test the nullspace property on A and show on some numerical examples that these relaxation bounds can prove perfect recovery of sparse solutions with relatively high cardinality.
The J&N code in the last version did not run to full precision. This version thus includes updated (and significantly different) numerical results comparing both LP and SDP relaxations. Numerical results on the randomization lower bound were also added
What is also noteworthy and wasn't available in previous versions of the draft is the attendant code. The NSProp implementation is now available here:
Oustanding! Now let me point to the conclusion of the paper:
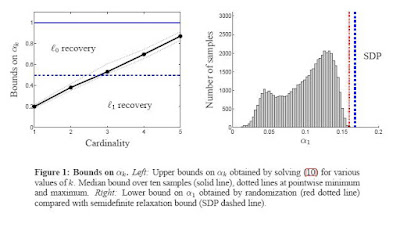
We have detailed a semidefinite relaxation for the problem of testing if a matrix satisfies the nullspace property defined in Cohen et al. (2006). This relaxation matches the linear programming relaxation in Juditsky and Nemirovski (2008) when k = 1 but is not as tight for larger values of k. On the other hand, it also produces a tractable lower bound on the objective value which does not require solving a (potentially exponentially long) sequence of convex optimization problems as in Juditsky and Nemirovski (2008). In particular, our results prove that both LP and SDP relaxations on α1 are tight for the Gaussian and Bernoulli matrices tested here. We can also remark that the matrix A only appears in the relaxation (9) in “kernel” format A^T A, where the constraints are linear in the kernel matrix A^T A. This means that this relaxation might allow sparse experiment design problems to be solved, while maintaining convexity. Of course, these small scale experiments do not really shed light on the actual performance of both relaxations on larger, more realistic problems. In particular, applications in imaging and signal processing would require solving problems where both n and k are several orders of magnitude larger than the values considered in this paper or in Juditsky and Nemirovski (2008) and the question of finding tractable relaxations or algorithms that can handle such problem sizes remains open. Also, while empirical evidence suggests that our relaxation is quite tight for certain types of random matrices (and that it matches the LP relaxation on α1, which achieves order √k for matrices satisfying the restricted isometry property at order k), we could not, at this point, produce explicit bounds on the recovery threshold of this semidefinite relaxation.
I realize that more realistic problems might be out of reach because of time constraints, but then again, I believe it is just a question of time that we either have a theoretical breakthrough in this area or we have more powerful tricks and machinery to compute this bound in a short amount of time for large rectrangular matrices. For those of you who just find out about this subject, you may to check my previous entry on this issue. On that subject, I am still looking to the re-availability of the J&N code.
No comments:
Post a Comment